Difficulty:Easy
Problem Statement
Given the root of a binary tree, return the inorder traversal of its nodes’ values.
Example 1:
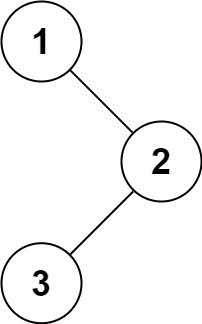
Input: root = [1,null,2,3]
Output: [1,3,2]
Example 2:
Input: root = []
Output: []
Example 3:
Input: root = [1]
Output: [1]
Approach & Explanation
We use Recursion for the trivial solution of this problem. Check Tree Traversal Theory for what Inorder traversal is. Basically its Left subtree - Root - Right subtree. Our function for solution calls itself recursively for left subtree and right subtree.
A list result is initialized to collect node values in the correct order.
Base Case: If the current node is None, an empty list [] is returned.
The extend() method is used to add the results from left and right subtrees to result. After the recursion completes, the result list contains the nodes in inorder sequence.
Solution
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
result = [] # This list will hold the inorder traversal result
if not root:
return result # If the root is None, return the empty list
# Recursively traverse the left subtree and extend the result list
result.extend(self.inorderTraversal(root.left))
# Append the value of the current node
result.append(root.val)
# Recursively traverse the right subtree and extend the result list
result.extend(self.inorderTraversal(root.right))
return resultComplexities
Time Complexity:
Space Complexity:
For the nodes, we do have to visit all of them to ‘traverse’ through. In a recursive solution, all the roots are called onto the memory stack so in worst case it is also .
Possible Confusion
- Why Doesn’t result Get Messed Up?
- Local Scope: Each recursive call creates a new result list in its own scope. When a recursive call returns, the parent function’s result list is extended with the returned values.
- No Re-initialization: The
resultlist in the parent call (the og one) is not re-initialized or overwritten during recursion, preserving its contents.
- Handling Empty Lists with
extend()
- Empty Lists: When a subtree has no nodes (None), the recursive call returns an empty list []. Using
extend()with an empty list has no effect on result, so it remains unchanged.
Further Challenge
Recursive solution is trivial, could you do it iteratively?
For this we use a stack to simulate the call stack used in recursive calls. In this example we can just use a list for our stack. This iterative approach simulates the recursive process using a stack, making it a practical solution when recursion is not desired or when dealing with very deep trees where recursion might cause a stack overflow. The stack helps ensure that the nodes are processed in the correct inorder sequence.
Process:
- Start from the root node and push all the left children onto the stack. So keep going left until it hits
null - Start to Pop from the stack. Whenever popped, add the node value to the result list. Then move to the right subtree.
- Repeat the process until all nodes are visited and the stack is empty.
The result list stores the node values in the correct inorder sequence.
Iterative Code
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
result = []
stack = []
current = root
# done only when both empty
while current or stack :
# keep going left
while current:
stack.append(current)
current = current.left
# the following order matters otherwise result appends None
current = stack.pop()
result.append(current.val)
current = current.right
return resultComplexities
Time Complexity:
Space Complexity:
Confusing bits
- If the root is None, the initial while current or stack: condition fails, and the function returns an empty list immediately (handles empty tree).
- When we move to right, we don’t append it to stack in the outer while loop because it will be done in order within the inner loop
- When current is None, it means we’ve reached the bottom of the left subtree. We then pop the stack to move up the tree and visit the parent node.
- After visiting a node, the algorithm moves to its right subtree by setting current to current.right.
Outer while Loop: while current or stack:
Ensures that the traversal continues as long as there are nodes to process.
current: Represents the current node being processed. Ifcurrentis notNone, the traversal continues to push left children onto the stack.stack: Holds nodes that are waiting to be processed. Even ifcurrentbecomesNone(when reaching the end of a branch), the loop continues as long as there are nodes in the stack.- The loop guarantees that all nodes are eventually visited, even when navigating back up the tree after reaching a leaf.
Inner while Loop: while current:
Traverses the left subtree of the current node, pushing all left children onto the stack.
- The loop continues as long as
currentis notNone. - In each iteration,
currentis pushed onto the stack, and thencurrentis updated to its left child (current = current.left). This loop helps navigate down to the leftmost node of the current subtree, ensuring that left children are processed before the root.
Exiting the Inner while Loop
The inner while loop exits when current becomes None, meaning the leftmost node has been reached.
- The node at the top of the stack (which is the last left child processed) is popped.
- This node’s value is added to the result list (
result.append(current.val)). - The traversal then moves to the right subtree of this node by setting
current = current.right.
Returning to the Outer while Loop
- Even after processing a node, the outer loop continues if there are more nodes in the stack or if
currentis updated to a new node (from the right subtree). - The algorithm repeats the process of pushing left children, processing nodes, and moving to right subtrees until all nodes are processed and both
currentisNoneand thestackis empty.
This structure ensures that nodes are visited in the correct inorder sequence (Left, Root, Right) without recursion.