Binary trees are a fundamental data structure where each node has at most two child nodes: a left child and a right child.
Types
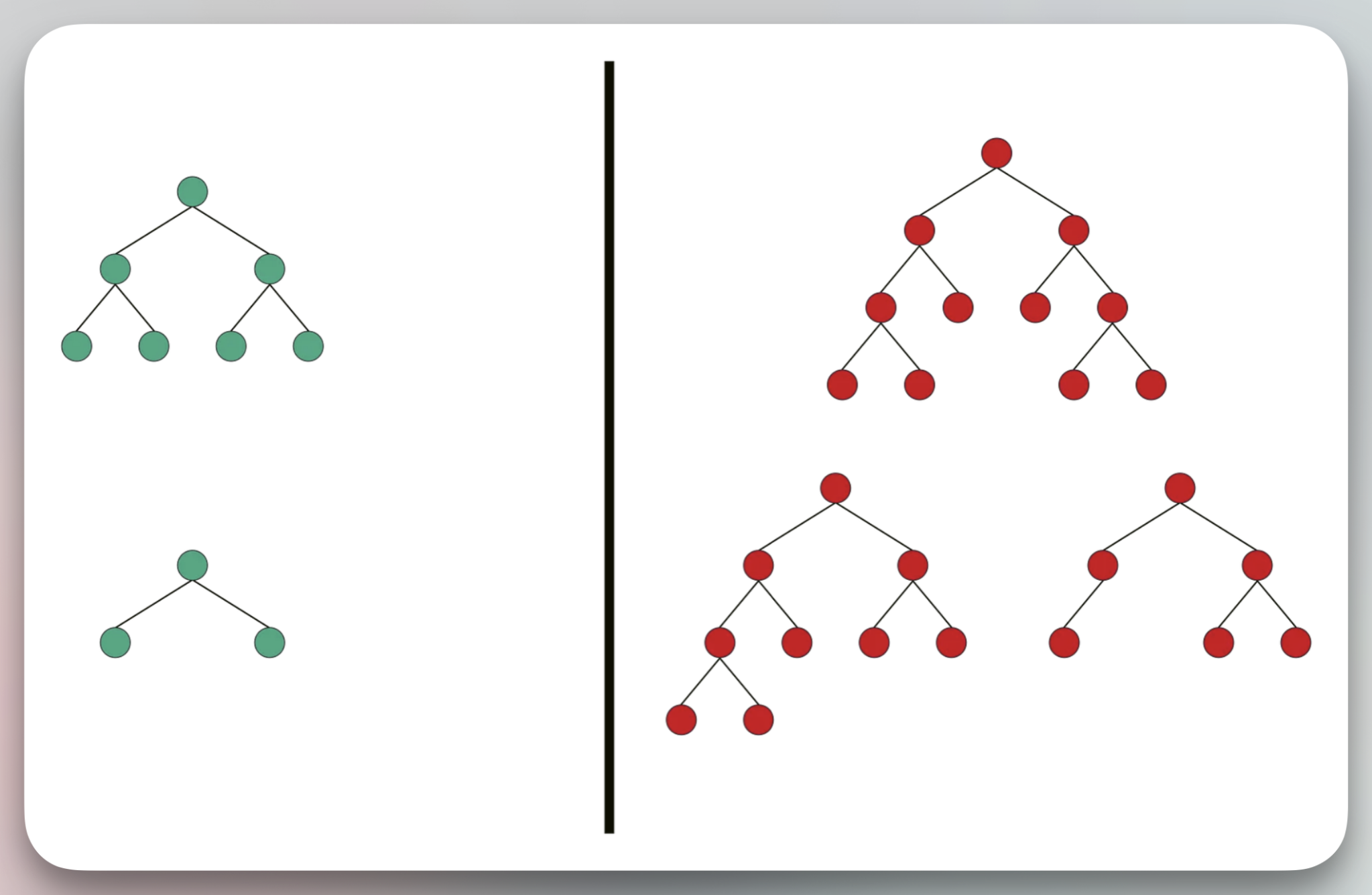
The major types of binary trees are briefly explored below with pictures to illustrate valid/invalid examples.
Note: In the pictures below, the green examples are valid and red ones are invalid
1. Full Binary Tree:
Definition: Every parent/internal node has either two or zero children. OR All nodes have two children but the leaves have zero children
Properties:
- Dense structure, minimal wasted space.
- Useful for efficient implementations of heaps (priority queues).
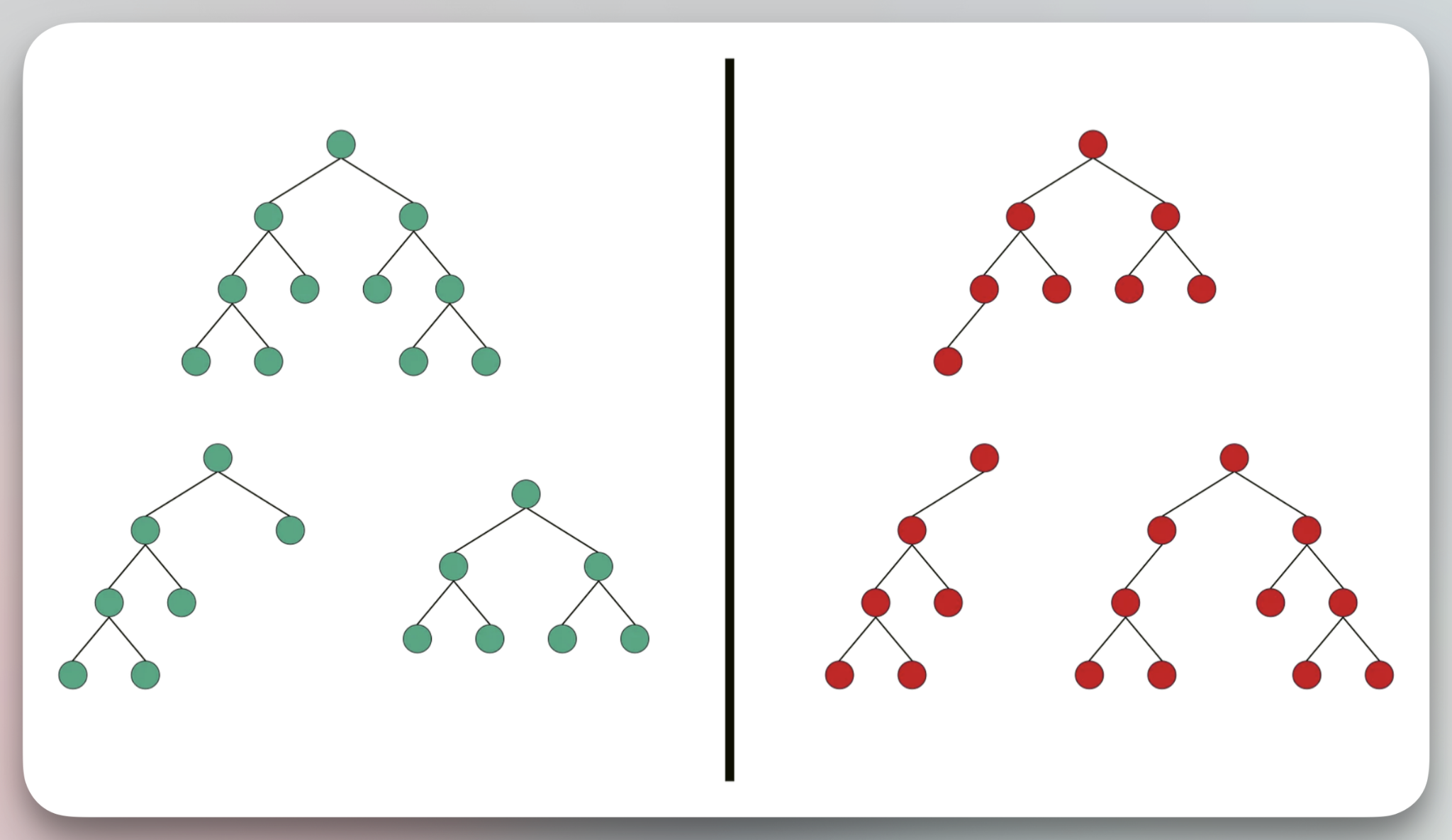
Note : For the following definitions below, try to relate their definitions in terms of different ‘level’ completion.
2. Complete Binary Tree:
Definition: All levels are completely filled with the exception of bottom level. It could be filled in which case it’s also a full tree. If not filled, then the bottom level is filled from left to right.


Properties:
- Useful for efficient array-based implementations of trees.
- Not necessarily a full binary tree (some internal nodes might have only one child).
3. Perfect Binary Tree:
Definition: A combination of full and complete binary tree. Every internal node has two children, and all leaves are at the same level.
Properties:
- Least number of nodes for a given height.
- Not always achievable in practice as adding/removing nodes might break the perfect structure.
4. Binary Search Tree (BST):
Definition: A special kind of binary tree where each node’s value is greater than all its left children and less than all its right children.
Properties:
- Enables efficient searching (average time complexity of O(log n) for search, insertion, and deletion).
- Useful for sorting and keeping data organized.
5. Self-Balancing Binary Search Tree (e.g., AVL Tree, Red-Black Tree):
Definition: A BST variant that automatically balances itself after insertions or deletions to maintain a specific height difference between subtrees.
Properties:
- Guarantees O(log n) search, insertion, and deletion even in worst-case scenarios (unlike standard BSTs).
- More complex to implement compared to BSTs.
Choosing the Right Binary Tree:
- The best type of binary tree depends on the specific application and desired operations.
- Full binary trees are good for efficient heap implementations.
- Complete binary trees are useful for array-based implementations.
- BSTs are excellent for searching and keeping data sorted.
- Self-balancing BSTs offer guaranteed worst-case performance for search, insertion, and deletion.
For tree traversal methods, check Tree Traversal Theory.