104. Maximum Depth of Binary Tree

Difficulty:Easy

---

Problem Statement

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

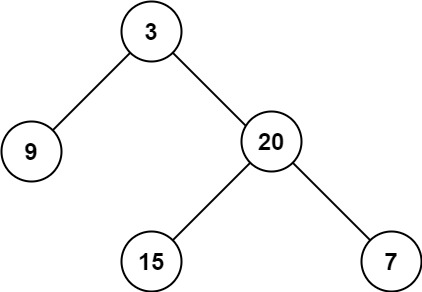
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Problem Link

---

Approach & Explanation

There are three main ways to approach this problem -

1. Recursive DFS
2. Recursive BFS (level-order traversal)
3. Iterative DFS

Among them I personally find the BFS approach to be the simplest and most intuitive to remember so that’s the one used here. However for learning purposes other methods should be explored as well. Note that all three of these methods are identical in terms of performance and memory complexity.

The BFS solution is very easy if we remember the typical BFS approach using a heap.

• Keep main condition as - until heap is empty, repeat
• Enter root in heap
• For the current length of heap, keep popping (FIFO) nodes from heap
• If there are any children append it to the heap
• Once this length has been process, increase the counter and repeat until heap empty

---

Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        counter = 0
        container = deque([root])
        while container:
            for i in range(len(container)):
                current = container.popleft()
                if current.left:
                    container.append(current.left)
                if current.right:
                    container.append(current.right)
            counter +=1
        return counter
        

Complexities

Time Complexity: $\mathcal{O}(n)$
Space Complexity: $\mathcal{O}(n)$

All the nodes require a visit exactly least once (traversal) hence the time complexity is linear.

---

Possible Confusion

• deque only takes iterable so root is enclosed in a list
• Outer while loop ensures all the nodes are processed
• Inner for loop ensures a single level is processed at once
• remember to pop after the for loop starts (levelwise pop starts)